Thank you Pete.
Here is my summary of the argument, and my new experimental result which agrees closely with my thin membrane model of the bicycle tyre and differs from the motorbike tyre theory. I see no reason to expect that the coefficient of friction in normal conditions is small enough to allow much slipping to take place, which might affect the calibration constant by a large amount. I do not rule out very small effects due to slipping right at the edge of the contact patch.
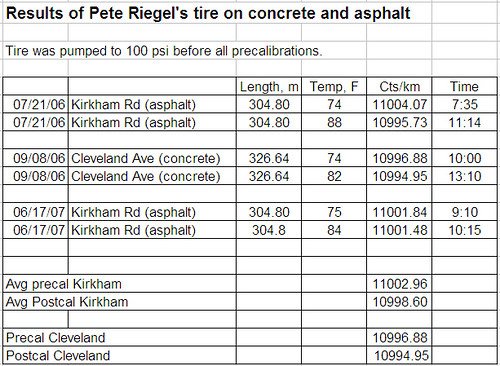
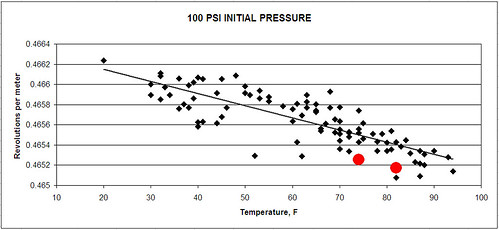
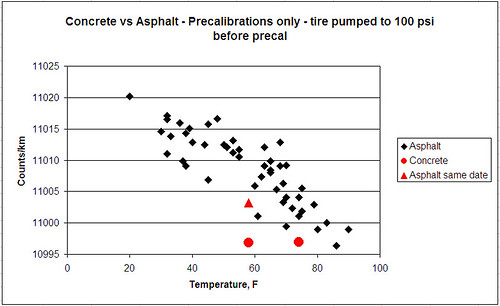
Several times I have noticed that measurers have claimed that the coefficient of friction between the bicycle tyre and the road surafce affects the calibration constant, and I agree that the could be effects especially on icy roads. However, I have always been of the opinion that for ordinary road surfaces and for bicycle tyres like a racing or touring bike, there was not much slip in the contact patch between the front wheel tyre and the road. I was also of the opinion that of far greater importance in its effect on the calibration constant is the surface texture of the road. Ten years ago, I wrote a series of articles on this which appeared in Measurment News. Copies of those articles can now also be down loaded from
http://coursemeasurement.org.uk/reports/3 days ago Jim Gerwick made a posting on this board
https://measure.infopop.cc/eve/forums/a/tpc/f/69510622/m/8761022113 in which he said
quote:
Also, I think the different friction coefficient for synthetic rubber vs. asphalt may be a factor.
I replied saying
quote:
Incidentally, I don't think anyone has proved that the coefficient of friction makes a difference, although I do suspect it may possibly make a contribution to the variation in calibration constant on different surfaces. What we do know for sure is that the roughness of the surface has an effect on the calibration constant. I took data on this including on a rubber track over ten years ago.
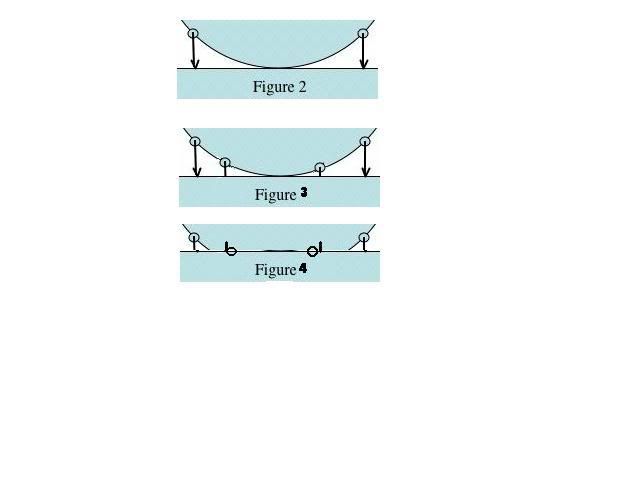
Mark Neal then entered the discussion and suggested that the tyre might be slipping over the road surface at some points in the contact patch, since the ground has to provide forces to which compress the tyre wall in the area of the contact patch, in order that the tyre can "squeeze" through the contact area (this is my short interpretation of Mark's theory). Mark bolstered his theory by quoting from a book about motobike tyres. This book quotes an approximate equation:
Ro=R-(R-H)/n where R is is the unloaded radius of the tyre, Ro is the effective rolling radius (ie the radius which gives the effective circumference and hence the calibration constant of the tyre), H is the height of the axle above the ground, and n is a constant which has the value of approximately 3 for a motor cycle tyre.
Models of car and presumably motor bike tyres are quite different to my simple model of a pneumatic bicycle tyre. I assume the bicycle tyre inner tube and tyre casing behave like a perfect thin membrane which can only transmit forces from one part of the tyre to another part in the plane tangential to the plane of the membrane at any point. In the theory of car tyres the flexural stiffness of the tyre wall plays a more signicant role, and when it is bent the tyre wall can transmit bending forces from one part of the tyre to another. It is like the difference between a thin walled toy balloon and a stiff walled ball - the former being my concept for the bicycle tyre, the latter more like a car tyre.
If my model of the bicycle pneumatic tyre rolling along the road is correct, then I predict a value of n=1. If the theory Mark suggests applies, then the value will be larger than 1, perhaps as large as 3 for a situation like a motorbike tyre.
This morning I carried out an experiment to determine n for my tyre.
Some time ago I measured the difference between my riding calibration: 10901.8 cts/km, and my walking calibration:10802.7 cts/km. The riding calibration is 0.92% larger.
The J-O and J-R counters produce 260/11 counts per revolution of the front wheel. So we can calculate the effective rolling radius for each case, obtaining the following values:
Riding Ro = 345.1 mm Walking Ro = 348.2 mm
Now the value of the walking Ro, will be very close to the value R, the unloaded radius of the tyre, because when walking the load on the front wheel is only a few Kgs of the bike, whereas when I ride about 25kg of my weight is loaded on the front wheel. So for this approximate calculation I am going to assume that the walking Ro = R.
This morning I measured R-H by photographing how much the tyre compressed when I added my weight in the riding postion. I can give full details of the experimental set up separately, but basically my son photographed the movement of a pointer attached to the steel tyre rim above the contact patch relative to a vertical ruler which was attached to the ground. We took 3 pairs of readings - we can easily read the position of the pointer in the photographs with a precision of 0.2mm.
The results were :
Loaded: 15 mm 14.8 mm 14.5 mm Unloaded: 18.3 mm 18.4mm 18.3mm (N.B. the zero of the scale was above ground level)
The average measured value of R-H is thus 3.57 mm
Substituting in the rearranged formula, n=(R-H)/(R-Ro), we get n= 3.57/3.1 = 1.15. This is encouragingly close to 1 which is predicted if my thin membrane theory applies. In fact the difference between 1.15 and 1 could easily be accounted for by not measuring the weight of the bike, and various small experimental errors. Notice I got a range of values from the 3 pairs of measurements which could easily account for being the measured value of n differing slightly from 1.
What we can say absolutely for sure is that motorbike type of situation with n=3 does not apply to my bicycle tyre.
I conclude that the coefficient of friction between the bicycle tyre and the road is high enough in ordinary conditions to prevent the tyre in contact with the ground sliding relative to the ground. Except for possible small effects at the edge of the contact patch, the calibration constant will be independent of the coefficient of friction for normal roads. However, this may not remain true on icy roads with a very low coefficient of friction when even the thin wall of the bicycle tyre may produce effects similar to that seen in car and motor bike tyres.
**************I have now put up some pictures of this experiment at
the coursemeasurement.org.uk website *******