Pete suggests that riding downhill causes less weight on the front wheel, while the opposite is true for riding uphill. This would mean that riding in the downhill direction on a cal course would give more counts than riding uphill on the same course, and this has, in fact, been observed.
What has not been observed, or proven, is the idea that if you do an equal number of uphill and downhill rides on a cal course, this hill effect will cancel out, and you will get the same cal constant as you would on a flat course.
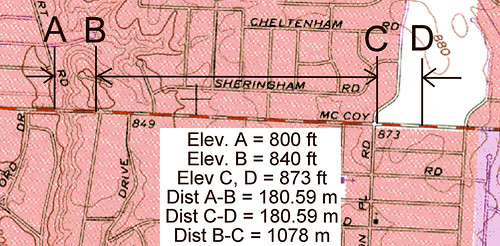
I decided this was worth testing. I have a cal course in front of my house that is 400m. The 200m on the west end has an elevation change of about 4m. The 200m on the east end has an elevation change of about 1.5m. I rode a total of 16 rides (8 out and 8 back) on each of the two 200m sections.
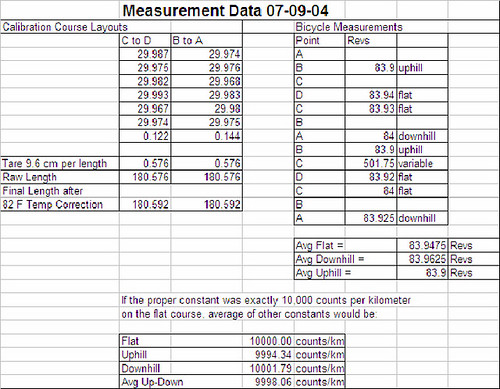
Here's the results

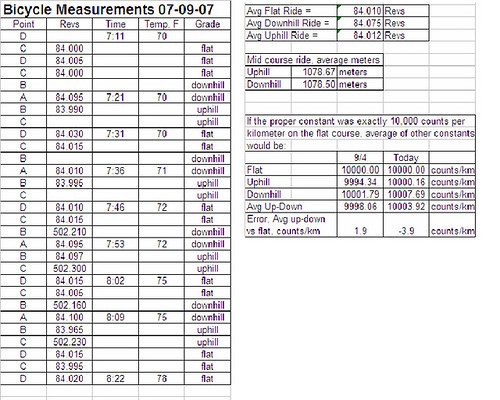
After I completed the experiment I realized that the pressure in my tire, 50psi, was on the low end. On another day I repeated the experiment with a higher pressure of about 63psi (the recommended pressure for my mountain bike tire is 35-65psi).
Here's the results from that second test.

The first thing we can observe is that downhill rides do result in higher counts than uphill rides, as expected. This was true for the hilly 200m section, but was also true for the "flat" 200m section, as the return direction on this course was downhill (by 1.5m) and gave a higher count than the uphill direction.
The second, and much more surprising finding, is that the uphill and downhill effects do not appear to cancel themselves out. In both experiments (lower pressure and higher pressure) the average cal constant on the hilly course was about 10counts/km lower than the average cal constant for the "flat" course. This is a huge difference of nearly the entire SCPF!
This experiment, along with the previous one on cal course length, suggests that you will get a more accurate cal constant by using a short, flat cal course than you will using a long, hilly one.