A discontinuity will occur here. A very long email discussion has just taken place involving mainly the Eastern certifiers and some others (although most of the Western certifiers won't have seen it). The email discussion was on the topic of suggested guidelines that Duane prepared on how to complete certificates. The discussion focused mainly on drop and separation -- how many decimal places to write, and how accurately we can obtain them. It was suggested that we continue the discussion here, by copying emails to this board, so I will do that. This will be a very long post, as I will copy a number of emails here.
_____________________
We have a number of issues here: How much accuracy can we obtain in calculating drop and sep, and how much accuracy do we
need in these values? Also, as one aspect of the first issue, a reason why some people may resist Duane's rounding suggestion is that he proposes rounding not only the final result of drop & sep calculations, but also rounding some of the
intermediate results which, in some cases, may significantly alter accuracy of the final result.
I'll start with this matter of rounding intermediate results. For example, Duane suggests rounding the individual Start and Finish elevations to whole meters before computing Drop. As an analogous situation, have you ever considered why, in measuring courses, we work with a "constant" in counts/km (or counts/mile) instead of alternative measures such as counts/meter or meters/count. Conceptually, these alternative measures are just as good for illustrating the principle of wheel measuring. But, in practice, if you worked in counts/meter or meters/count, you probably wouldn't carry enough decimal places, and because of that intermediate rounding, your final result would be totally inadequate for the purpose of course certification.
As a result of Duane's suggestion to round individual elevations to whole meters before computing drop, the drop computed this way may not agree (to a desired number of decimal places) with the drop computed from original elevation data without intermediate rounding. As one possible solution, assuming original elevation data were in feet, I know that some of you will suggest simply leaving them in feet when writing the certificate. For myself, I'll always convert to meters. However, I may need to reduce the amount of intermediate rounding to obtain good enough agreement of the calculated drop. For example, rounding those individual elevations to half-meter precision instead of whole meters may do the trick.
Regarding Justin's suggestion about significant figures, the calculation methods on the indicated website --
http://calculator.sig-figs.com/ -- can be considered a "quick and dirty" method that often keeps roughly the correct number of digits consistent with accuracy of the data. For the case at hand, however (drop and sep), it's easy enough to do a somewhat more rigorous uncertainty analysis, as opposed to the quick & dirty sig fig method. I won't present the analysis here (I may do so in a later message). But as results, I conclude that if elevations come from a source like Google Earth, we can justify only one decimal place for short courses like 5 km although, using the same Google Earth elevations, we can probably justify two decimal places for a long course such as a marathon.
As far as I know, nobody has mentioned this interaction with the course length. Of course, the best way to improve the accuracy of calculated drop is to have more accurate elevation data to start with. But, for elevation data of given accuracy level, we get more accurate drop results for longer race courses.
How accurate do we need the calculated drop to be? In most cases, I see no reason to go beyond one decimal place. But if the drop is very close to the 1 m/km limit, it's reasonable to try for a 2nd decimal place. Doing this in a meaningful way may, however, require more accurate elevation data than we usually have available.
Turning to separation, we get two very different sorts of situations. On the one hand, when start and finish are close together, the distance between them may have been taped, and is therefore known very accurately. In these cases, we can, in principle, compute the percentage separation with considerably better than one decimal place, although I see no reason why we'd need that information. On the other hand, when separation is larger, the figures supplied by measurers are often very rough estimates. For example, a measurer may write something like a "quarter-mile" or "half-mile" which are just rough guesses.
In the first case, when the start-finish distance has been taped, I suggest writing this accurately known distance in the "Straight line distance between start & finish" space -- in meters and
not rounded to whole meters. Writing this distance accurately does no harm, and in some cases (e.g., a loop course with separated start and finish), it can be the crucial information needed to set up the course accurately (in such a case, it's presumably also on the course map, but it does no harm to document it in this additional place).
While I would write the "Straight line distance..." with enough digits to match the accuracy available, I can't see any reason why we'd want more than one decimal place in percentage separation values. The only case where we might be tempted to write more than one decimal place is when the separation is extremely small (but non-zero), because we shouldn't enter the separation as exactly zero unless the course truly has a common start/finish. But there's a simple solution for this case: For any non-zero separation which is less than 0.1%, simply round it
upward to 0.1%. And, by the way, I seem to recall that Ken Young used this approach in the course list long ago.
For the case of large separations, when a measurer has provided only a rough estimate, I also tend to disagree with Duane's recommendation to round the "Straight line distance" to whole meters, but for an opposite reason. For example, if the measurer estimated a "quarter-mile," the metric conversion in whole meters (402 m) would overstate the accuracy. So, instead, I might round it to 400 m or 0.4 km.
For these courses with large separations, the most accurate way to determine the separation (short of professional surveying) is probably with a tool like Google Earth. But even if this is done very carefully, it's probably not practical to determine the percent separation with even one decimal place; i.e., we'd probably just have to express the separation as a whole number. If the separation turns out to be very close to 50%, and we can't resolve it ourselves, the only solution may be professional surveying.
_________________________
I'd like to expand a little on the long message I sent last night. In connection with separation, I wrote near the end that for large separations, the best we can do (short of professional surveying) is with a tool like Google Earth, and when doing this, we probably can't get the percent separation better than whole numbers. After sending this, it occurred to me that we may be able to do better if we have coordinates from consumer-level GPS devices. To compute the straight line (or more generally, great circle) distance between two points with known latitude and longitude, there are various calculators, e.g., see
http://www.movable-type.co.uk/scripts/latlong.htmlI'll illustrate with course CO11036DCR which is an interesting case I happened to discover by doing a search for courses with Drop entered as exactly 1 m/km (but my comments here will be about the separation of this course, not its drop). As one interesting aspect, it's listed incorrectly in the database as a 5 km course although it's really a 5 mile course (Gene, you need to fix this). As another error, the cert number written on the map is CO10036DCR although it's really CO11036DCR. You can view the map and certificate at
http://www.usatf.org/events/co...?courseID=CO11036DCR Duane helpfully provides GPS coordinates on the map. From the start and finish coordinates, the calculator cited above provides straight line distance 5.087 km. And since it's a 5 mile (8.04672 km) course, the separation works out to 63.2%. I also obtained a very similar result from Google Earth. On the certificate, the straight line distance was entered as 5430 m and the separation was entered as 67.5%.
________________________
Interesting note about using Google Earth in checking separation: When checking a "Line" distance in Google Earth, it displays two distances now, both "Map Length" and "Ground Length." This appears to be a new feature that I hadn't noticed before. My interpretation is that "Map Length" is the distance calculated from latitude and longitude along a surface at mean sea level, while "Ground Length" is adjusted for altitude. At the altitude of Denver, the Ground Length is about 1.00025 times as great as the Map Length. Of course, the difference between these figures is less than the SCPF we use in measuring the course distance.
________________________
To Bob T, Mark, etc.
I think it's pretty clear what the "Ground" length in GE means. First, as you can tell, it's purely a two-point measurement; it's calculated entirely from coordinates of the two endpoints, and doesn't pay any attention to what's in between. But when it calculates this two-point distance, it takes account of two kinds of elevation effects:
1) The Pythagorean slope effect if there's a noticeable elevation difference between the two points. That's what you demonstrated, Bob, in your example with a 134 m elevation difference over a horizontal distance of about 800 m.
2) The effect of being farther from the center of the earth (even when both points are at the same elevation), so that a given angle from the center of the earth (i.e., given change in latitude & longitude) subtends a greater arc distance. Here, the ratio of distance covered, compared with distance at sea level, is roughly (R+h)/R where R is the radius of the earth and h is your elevation above sea level.
The second effect is the one I had in mind when I wrote that in Denver (elevation about 1.6 km), ground distances are greater than map distances by a factor of about 1.00025. It also explains your second example, Bob, assuming that both points are at about 250 m elevation.
In that 2nd example (with elevation change about 7 m in horizontal length about 3772 m), the Pythagorean effect amounts to only about 6 mm, and you don't need a super calculator to show it. You can get it from the approximation that if "a" is much greater than "b" then:
sqrt (a^2 + b^2) is approximately a + (b^2)/(2a)
where it should be noted that the small size of the (b^2)/(2a) term is the reason why the "offset" technique we often use while measuring (to avoid riding dangerous tangent lines) is effective.
To David:
Yes, we need to seriously investigate the sources of drop and separation data to provide the data needed to support records.
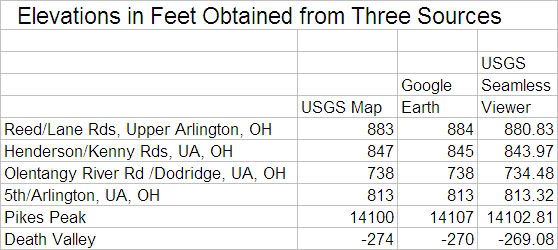
For drop: My feeling is that GE is probably good enough for most cases, when drop isn't very close to the 1 m/km limit. For drop closer to 1 m/km, it may still be good enough for longer courses (e.g., marathons) but it breaks down for shorter courses (e.g., 10 km). The USGS national map viewer at
http://viewer.nationalmap.gov/viewer/ is probably a little more accurate than GE. Among other sources, I don't have much feel for accuracy of elevations from consumer-level GPS, but my hunch is that they're not as good as Google Earth or USGS. I also don't have any feel for accuracy of elevation data that municipal agencies may have (which you said you'd try using, David). The ultimate accuracy would be by professional surveying.
For separation: I think GE and latitude-longitude coordinates from consumer-level GPS are both pretty good, and can probably settle the matter in most cases. But if it's really close to the 50% limit, professional surveying may be required.