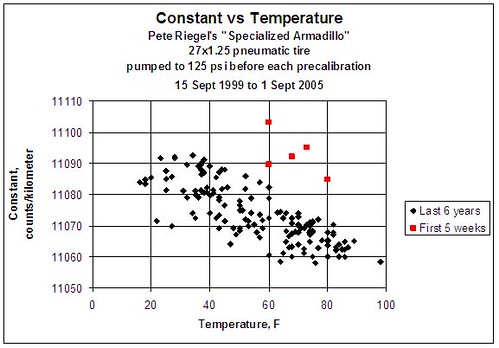
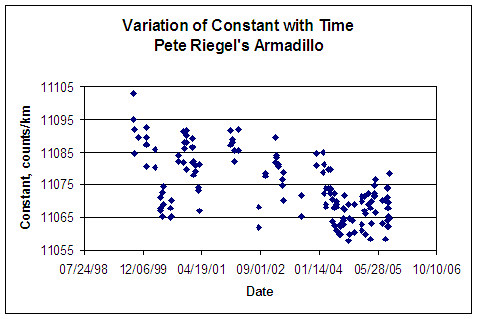
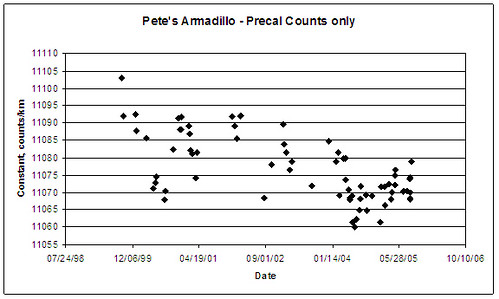
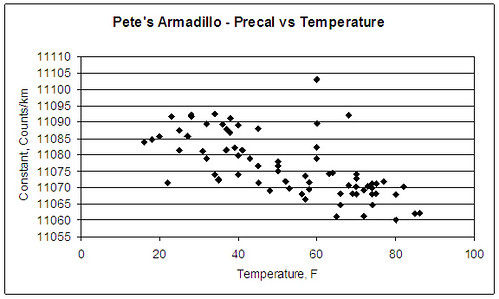
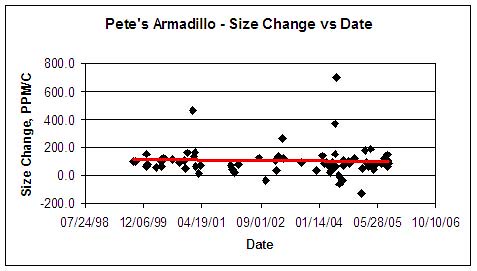
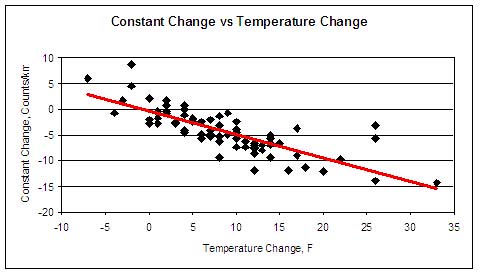
Here is a complete history of my former pneumatic tire. All calibrations are shown, both precals and postcals. I've started a new series with new tires, but thus far have only two calibrations.
Note: the first five calibrations took place just after installation. I think the tire, under its newfound inflation stress, spent time creeping into its equilibrium size during the first few weeks.
I remain puzzled as to why the tire size should have gotten larger as temperature increased. After all, the initial pump-up pressure was constant throughout. I had thought that rim expansion might explain it, but the expansion, while in the right direction, was not nearly enough to explain it.