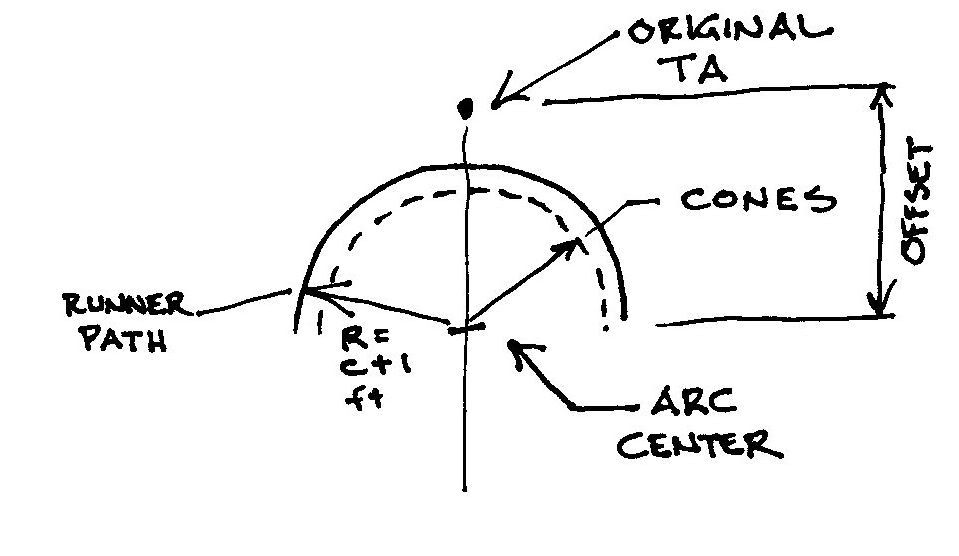
Using your calibrated bike, lay out your TA as though it was a single point, and there was no arc. Now see how much room you have and what you want your arc radius to be. Call the arc radius “C.” Remember than the runners will run 30 cm (1 foot) outside the arc. This radius is R (=C+1 feet)
The runners, running around the arc, will add distance to the true out-back. This will be equal to π (pi) times the radius they run. The deduction from the original TA point will be half this value, as it is this short out-back which you are removing and replacing with the arc.
The offset will be:
Offset = πR/2
Example: If the cone radius is 15 feet, the runner radius is 16 feet. The offset is π(16)/2 = 25.13 feet. Thus the arc center will be 25.13 feet short of the original TA.
Mark the new center and lay out an arc of paint dots where the cones should be.
The length of the arc will be πR, or 50.26 feet added to the course.
The deduction from the original TA is 2x25.13 feet, or 50.26 feet.


