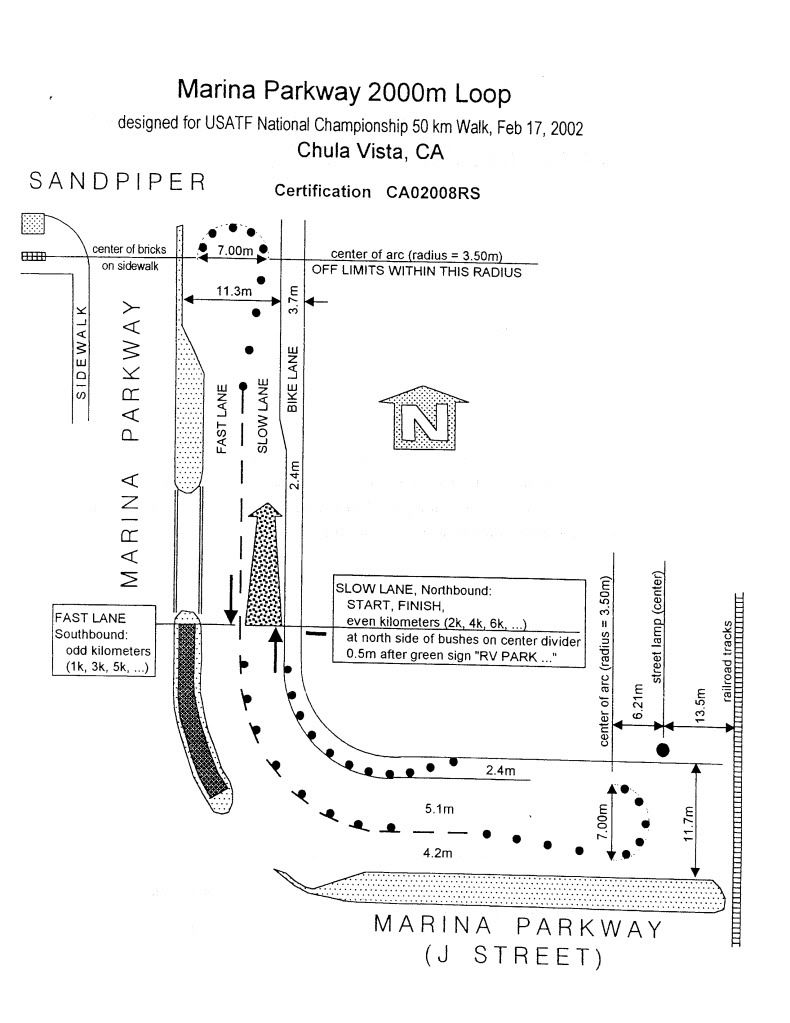
Here's and article on Race Walk Design written by Ron Daniel (IAAF Level-1 Race Walk Official)
RACE WALK COURSE DESIGN NOVEMBER 2007Ron Daniel Introduction: In this memo, I will describe the affect of tight turns and narrow race lanes on the performance of the athletes and judges in a race walking competition.
Discussion: I was a race walk judge at three international events (RW Challenge, Mexico, Japanese 20k Championship and Pan American Games) this past summer where the 2km loop had 2m radius turns on each end. The Japanese 20km Championship was being used as the test event for the IAAF World Championship in Osaka, Japan.
At the test event, in addition to the 2m turns, the racing lane was 3m wide (a 6m road with cones down middle). This 3m lane narrowed to 2m on one end as the course-reversed direction. The judges had access to a 4m wide sidewalk on each side of the road. The principal problems with 2m turns for the walkers are the inability to maintain racing speed and legal form. With 49 starters, the athletes were also very crowded during the first two laps (8+ for race). The only problem that the judges encountered was staying aware that the sidewalk had a 5-inch curb. In fairness to the athletes, the judges maintained a presence at the turns but did not over-judge the turns.
In a meeting following the championship (test event), the Japanese LOC agreed to increase the turns to 4m radii and widen the one turn lane to at least 3m. There was nothing to be done about the 3m width of the racing lane; this guaranteed very crowded racing throughout most of the two World Championship 20k races.
At the World Championships, the judges encountered a problem not known at the test event. Instead of the 4 m wide sidewalk, there were placed one-meter tall advertising boards one meter from the edge of the curb on both sides of the course (fig.1) for much of the 1km long course. This narrowing of the course for the judges impacts their ability to properly observe the walkers step progression; the difficulty increases as walkers begin to trail behind and the judges are now faced with walkers moving in two directions and the judges are wishing to observe the walkers in the farther lane. Advertising boards also ringed the turns and one was placed in the middle of the turns further affecting the judges viewing.

Figure 1. Advertising Boards on Course
Performance Impact: An athlete’s speed in a turn is affected by his ability to lean into the turn at a sufficient angle. This angle is dictated by the centripetal force a walker or runner must generate to negotiate a curve of a given radius at a given speed. The following analysis was initiated by Dr. Wayne Armbrust (PhD in physics with biomechanics expertise). Table 1 below shows a comparison between the lean-in angle for a 5,000m runner on an indoor 200m track of radius 21.3m, on an outdoor 400m track of radius 36.8m and a 200m runner on an outdoor 400m track.
Table 1.

When the 2m radius turn was proposed, we calculated that a 1hr 20min 20k walker would need to lean-in at a 41.5 degree angle in order to maintain his speed; more than 2 ½ times the lean-in angle for the sprinter. During the test event, many walkers were leaning-in at 20 degrees. (Fig 2.) Even so, with a 2m-radius turn and 20 degree lean the walker will still loose valuable time in each turn. During the 20k on the Osaka course there were 17 turns which would result in a loss of 18.5 sec for the 1:20 pace walker and 12 sec for a 1:30 pace walker. This information was instrumental in having the LOC increase the turn radii.

Figure 2. 20k lean-in, 20 deg.
The most significant problem for the 20K walkers, throughout the test event, was the loss of form around the turn. Fig 3. Some walkers purposely walked a wider turn to try to minimize the problem. For every one meter wide, the walker adds over 3m per turn and after 17 turns more than 50m to the race.
The change to the 4m radius turns for the World Championships allowed the 20k walkers to race to their full potential (Chart 1. Lost time vs. lean-in angle) even though they still leaned in at 20 degrees. The 50k walkers had no time loss while leaning at 15 degrees; however, many walkers still walked wide (fig. 4). Bent knees in turns was noticeably reduced (as viewed on video).

Figure 3. Bent knee form in turn.

Figure 4. 50k Lean-in, 15 deg.
The necessary lean-in angle for 20k and 50k walkers vs. turn radii is shown in Chart 2.
The chart shows that the turn radius would have to be increased to 10m in order for the lean-in to be comparable to that of the 5,000m runner on a 400m track.
While lost time and bent knee problems were reduced on the 4m radii turns, there still exists additional performance impacting stresses. The first is the lateral stress due to the centripetal force required for the turn; this stress is proportional to the tangent of the lean-in angle. The lateral stress increases 3.5 times as the walker leans to 20 degrees versus 6.5 degrees (the lean-in angle of the 5000m runner). This is then coupled with the change in linear
Chart 1

Chart 2

motion around the turn creating rotational forces on the ankles, knees and hips. For example, a walker with a 1.35m step turning around a 4m radius has a 19.35-degree change of direction on each step. The lateral and rotational stresses become cumulative as the race progresses. These stresses directly contribute to the difficulty of the walker to maintain a straight leg in the turn while attempting to maintain speed. By comparison, the 5,000m runner with a step length twice that of the walker, only experiences a 4.2 degree change of direction on each step.
It’s difficult to quantify the affect of the narrow race lane on the athletes. In the men’s 20k race, through 10k there were about 20 walkers shoulder-to-shoulder within 3 seconds of each other. At one time early in the race, one of the men was forced onto the sidewalk for several strides. There is no way to assess the affect of the narrow course on the judges because each judge had nearly the same conditions and as was done at the test event, the judges were somewhat forgiving on the turns, only calling the flagrant bent knee transgressions.
Recommendations: When designing a course, my recommendation is that the turns be at least 5m in radii and the racing lane be at least 5m wide. Then there will be almost no slowing in turns and minimal lower leg stress due to excess lean-in and less crowding on the circuit. Judges should have at least 3m on either side of racing lane in order to properly view and assess the walkers. Advertising boards should not diminish the judges’ viewing anywhere on the course.
Conclusion: I’m well aware of the difficulty in locating a suitable venue for creating a viable racecourse. However, the design of any race walk course should take into consideration the affect on the athlete and impact on the judges. This should be true for any competition but most certainly for a major international competition. While this report focuses on race walkers, the loss of speed in turns is also true for runners.
# # #