Example of Pressure Predicted Postcal Using Pete's Data Trial kPa All over 750 Temp, F
3 04/08/06 7:45 771 464.90 464.90 38
3 04/08/06 15:00 800 464.62 464.62 50
3 04/09/06 7:55 760 465.12 465.12 32
3 04/09/06 16:00 805 464.48 464.48 58
3 04/10/06 7:30 777.5 465.03 465.03 38
3 04/10/06 7:35 775 465.12 465.12 38
3 04/10/06 15:50 812.5 464.35 464.35 66
3 04/11/06 7:30 760 464.97 464.97 40
3 04/11/06 16:05 825 464.21 464.21 76
3 04/12/06 7:30 785 464.67 464.67 59
3 04/12/06 14:17 805 464.30 464.30 69
3 04/13/06 7:25 760 464.93 464.93 48
3 04/25/06 9:10 680 465.58 58
3 04/29/06 7:00 620 466.04 45
3 04/29/06 13:42 675 465.47 68
3 05/02/06 6:55 640 465.92 60
From the above I see that if I use ALL the data points, rev/km increases 0.84 for every 10 kPa loss of pressure.
If I use only the data points above 750 kPa, rev/km increases 0.135 for every 10kPa loss of pressure. Above 750 is better, as it is closer to the normal range I use.
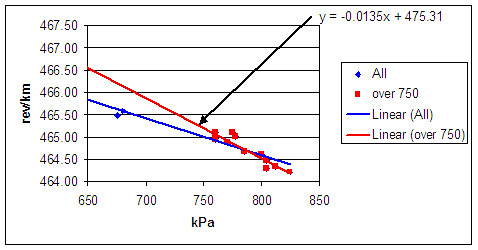
]
Consider the data of 4/9/06:
Precalibration = 465.12 rev/km at 7:55 AM at 760 kPa and 32F = 10993.67 counts/km
Postcalibration = 464.48 rev/km at 4:00 PM at 805 kPa and 58F = 10978.73 counts/km
Predicted postcalibration = 465.12 - 0.0135 x (805-760) = 464.39 rev/km =
10976.55 counts/km
So, we have an error of 2 counts/km between pressure-calculated postcal and actual postcal. This, in my opinion, is decent agreement.
Now consider the data of 4/10/06
Precalibration = 465.12 rev/km at 7:35 AM at 775 kPa and 38F = 10993.67 counts/km
Postcalibration = 464.35 rev/km at 3:50 PM at 812.5 kPa and 66F = 10975.44 counts/km
Predicted postcalibration = 465.12 - 0.0135 x (812.5-775) = 464.74 rev/km =
10984.73 counts/km
Here we have an error of 9 counts/km. This agreement is not so good.

 ]
] 